最近，以DeepSeek-R1表示的大规模推理模型可以描述为“流行”，但总的来说，这些模型的推理都是非正式推理。也就是说，他们主要通过自然语言进行推论。

但是，此推论模型具有缺点：很难通过机器自动验证。因此，在实际应用中非正式推理的可靠性大大降低了。这也将使研究人员更难进一步改善推理模型。

解决方案也非常直观：正式推理。

最近，由普林斯顿大学（Chen Danqi），Sanjeev Arora和Jin Chi领导的一支团队为自动定理校对开了一个正式的推理模型，该模型是在自动形式上证明数学问题的情况下生成的。索塔（Sota）被任命。精益工作簿中发现的代码，模型和新证明都是开源的！

首先，让我们简要解释什么是形式上的推理：简单地说，正式的推理是以机器验证的格式进行推理。在此类别中，更知名的证明助手包括Lean，Isabelle和Coq，所有这些都有自己的正式语言，可以以机器验证的方式表达推理。因此，培训LLM以这些形式语言写作是很重要的。

但是，培训LLM的另一个主要挑战是使用正式语言证明定理，即缺乏正式的数学陈述和证明。

对于用正式语言表达的定理，为他们编写证据非常苛刻，需要大量的现场专业知识。

因此，当前发表的正式语言数据集的规模非常有限。例如，Lean Workbook数据集总共有140K的正式语句，并且正式语句使用LEAN来指出问题，但没有得到证明。在这些陈述中，只有15.7k条具有正式的证据，这是由Internlm2.5-Stepprover和Internlm-Math-Plus发现的。此外，开放的引导定理数据集包含107K语句，其证明来自Mathlib44。

但是，团队观察到，Mathlib4的分布与一般解决问题的基准（例如广泛使用的minif2f）的分布明显不同。例如，minif2f中的陈述主要来自高中数学，需要复杂的推理技能来解决，而Mathlib4中的陈述则集中在简单的操作上，这些操作对高级数学的概念。此外，他们发现将Mathlib4数据纳入培训并不能不断提高模型在minif2F上的性能。

与形式语言中数据的稀缺相比，用自然语言编写的数学问题具有大量的数据储备。 “五三”堆在高中生的桌子上是富裕的矿山。 Numina数据集包含860,000个高质量的问答对，包括国内和外国小学和中学数学问题，国际奥运会竞赛问题以及合成数据。

为了将这些数据转换为可用的正式语言，研究团队培训了两个正式的转换器。一个基于精益工作簿中的非正式语言对，另一个是使用Claude-Sonnet-3.5注释的语言对训练的。下图显示了这些正式转换器的训练过程。

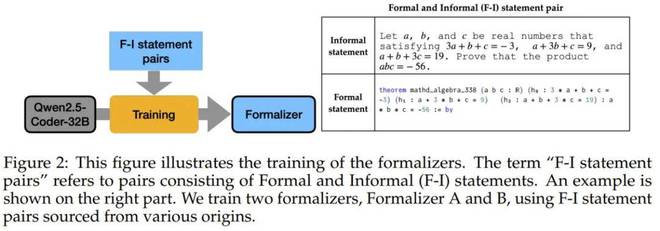
在这两个转换器完成正式化原始声明之后，该团队还使用LLM添加了验证，以确保正式的语句准确保留原始内容的含义，并成功地构建了一个包含164亿个正式语句的数据集。

使用这个大规模的正式定理数据集，研究小组采用了一种循环改进方法，称为专家迭代：首先使用现有最佳模型（DeepSeek-Prover-V1.5-RL）来尝试回答大量的数学问题，请收集正确的答案来训练新模型，然后使用新模型解决问题，不断重复该过程。经过8轮这样的“带来新的”训练，他们的新模型变得更加强大。下图显示了专家迭代的过程。

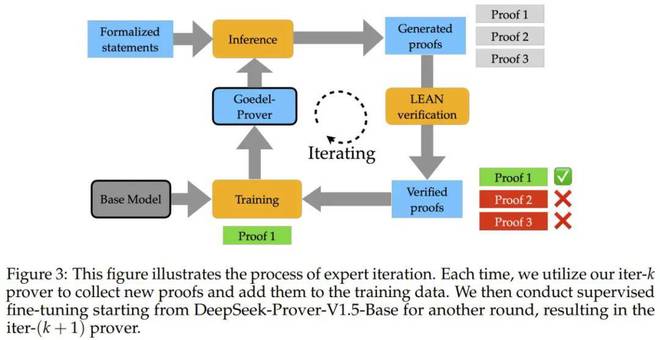
Goedel-Prover如何表现？

有多强大？如下图所示，在minif2f上，新模型的问题解决准确性比以前的最佳模型（DeepSeek-Prover-V1.5-RL）高7.6％。在@32、64和25600测试中，它们总是比DeepSeek-Prover-V1.5-RL更好。

新模型在精益工作簿数学问题库中成功解决了29.7万个问题，该问题几乎是其他顶级型号（Interlm2.5-Stepprover和internlmmath-plus）的两倍。在Putnambench上，新模型解决了7个问题（通过@512），排名排名第一。

普林斯顿的博士后研究员Yong Lin谈到该主题时说，他们目前正在开发Godel Piract的强化学习版本，并且还将拥有比以前更强大的检查点模型。此外，他们还将伴随164万个正式陈述，而开源此增强学习版本。

真的很令人兴奋。