机器之心报道

机器之心编辑部

Transformer 取得了成功。更普遍来讲，我们甚至能够把（仅包含编码器的）Transformer 当作学习可交换数据的通用引擎。因为大多数经典的统计学任务都是基于独立同分布（iid）的假设来构建的，所以很自然地可以尝试把 Transformer 应用到这些任务中。

经典统计问题训练 Transformer 有两个好处。其一，它能提升模型对经典统计问题的处理能力；其二，有助于模型更好地适应经典统计领域的任务和数据分布。

近日，MIT 的三位研究者 Anzo Teh、Mark Jabbour 和 Yury Polyanskiy 称找到了一个能满足“可能存在的最简单的这类统计任务”需求的东西，即 empirical Bayes (EB) mean estimation（经验贝叶斯均值估计）。

该团队称：我们觉得 Transformer 适合用于 EB。因为 EB 估计器会自然呈现出收缩效应，也就是会让均值估计倾向于先验的最近模式，而 Transformer 也是这样，其注意力机制倾向于关注聚类 token。可参阅论文《The emergence of clusters in self-attention dynamics》来了解注意力机制的相关研究。

该团队还发现，EB 均值估计问题具备置换不变性，所以不需要位置编码。

一方面，人们对这一问题的估计器有着强烈的需求。然而，令人困扰的是，即便最好的经典估计器，也就是非参数最大似然（NPMLE），也存在着收敛速度较为缓慢的状况。

MIT 的这个三人团队进行的研究表明，Transformer 的性能表现比 NPMLE 要好。并且，Transformer 还能够以接近 NPMLE 的 100 倍的速度运行。

总之，本文证实了即便针对经典的统计问题，Transformer 也给出了一种优良的替代办法，在运行时间和性能方面表现出色。对于简单的 1D 泊松 - EB 任务，本文还察觉到，即便只是参数规模极小的 Transformer< 10 万参数）也能表现出色。

定义 EB 任务

理解 Transformer 是如何工作的

论文第四章的目的是解释 Transformer 的工作原理，并且通过两个角度来达成这一目标。其一，他们构建了关于 Transformer 在处理经验贝叶斯任务时表达能力的相关理论成果。其二，他们运用线性探针来对 Transformer 的预测机制进行研究。

本文首先提及 clipped Robbins 估计器，它的定义情况如下：

得出：transformer 能够学习到任何精度的 clipped Robbins 估计器。也就是：

本文证明了类似的情况，transformer 还能够近似 NPMLE。也就是说：

附录 B 中包含完整的证明过程，而论文正文仅提供了一个大致的概述。

研究者接下来探讨了 Transformer 模型的学习方式。他们借助线性探针技术来对 Transformer 的学习机制进行研究。

这项研究的目的在于知晓 Transformer 模型是否会像 Robbins 估计或 NPMLE 那般工作。从图 1 的结果能够看出，Transformer 模型并非仅仅是对这些特征进行学习，而是在学习贝叶斯估计器具体是什么。

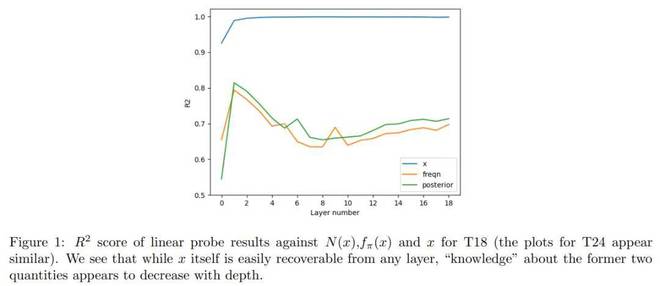
总结来说，本章证明了 Transformer 能够近似 Robbins 估计器。同时，本章也证明了 Transformer 能够近似 NPMLE（非参数最大似然估计器）。

此外，本文借助线性探针来证明，经过预训练的 Transformer 的工作方式与那两种估计器是不一样的。

合成数据实验与真实数据实验

表 1 展示了模型参数设置。本文选取了两个模型，依据层数分别给它们命名为 T18 和 T24，这两个模型各自大约拥有 25.6k 个参数。同时，本文还定义了 T18r 和 T24r 这两个模型。

在该实验里，本文对 Transformer 适应不同序列长度的能力进行了评估。图 2 把 4096 个先验的平均后悔值给报告了出来。

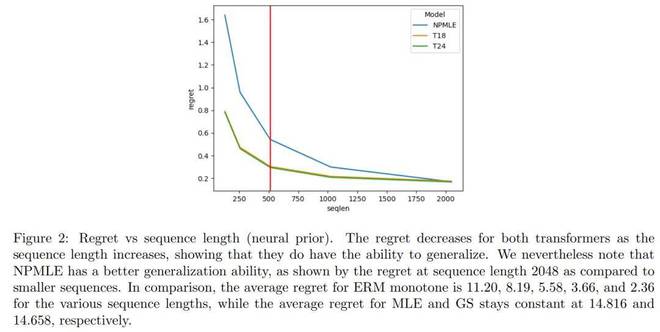
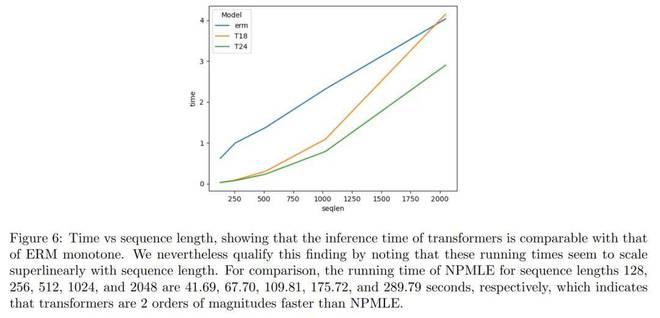
图 6 展现出 transformer 的运行时间和 ERM 的运行时间相差无几。

合成实验具有重要意义。Transformer 展现出了长度泛化能力。即便在未曾见过的先验分布上，当测试序列的长度达到训练长度的 4 倍时，它们依然能够达成更低的后悔值。这一点很重要，多项研究显示，Transformer 在长度泛化方面的表现各不相同，比如[ZAC+24, WJW+24, KPNR+24, AWA+22]这些研究。

本文最后在真实数据集上对这些 Transformer 模型进行了评估，目的是完成类似的预测任务。评估结果显示，这些模型通常比经典基线方法更优秀，并且在速度方面远远领先。

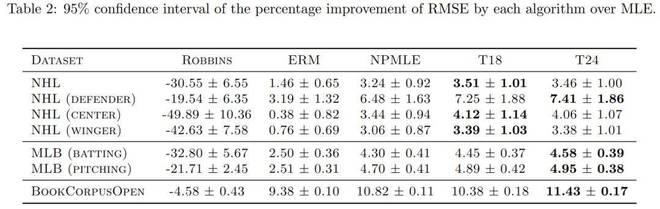
从表 3 能够得知，在诸多数据集中，Transformer 相较于传统方法呈现出显著的改进态势。

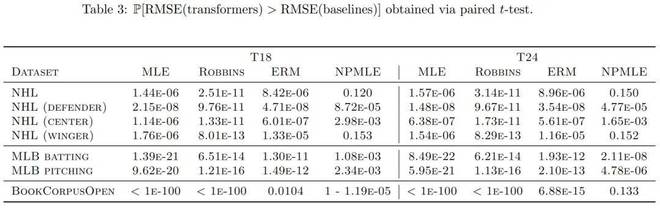
总之，本文证实了 Transformer 可以凭借上下文学习来掌握 EB - 泊松问题。在实验期间，作者表明随着序列长度的递增，Transformer 能够让后悔值降低。本文在真实数据集上证明了，这些预训练的 Transformer 在大多数情况下是能够超越经典基线方法的。