如果你知晓圆周率约为 3.14 ，那么你的数学程度至少达到了小学阶段的水平。正因如此，联合国科教文组织在 2019 年把每年的 3 月 14 日设定为“国际数学日”。

如果你知晓圆周率是一个无理数，也就是它属于无限不循环小数这一类型，那么就可以表明你的数学水平至少达到了中学阶段。基于此，即便再强大的计算机，也绝对不可能将π算到尽头。有时候，看到一群民间科学爱好者大肆谈论如何把π算尽，并且还大谈这会意味着揭开宇宙秘密等内容，着实让人觉得既好笑又无奈。

如果你知晓圆周率是一个超越数，也就是它并非任何整系数多项式的根，那么你的知识水准就超越了 99.9%的人。基于此，化圆为方通过尺规作图来完成是不可能的。任何仍在对这个问题或者三等分角、立方倍积等经典的不可能问题进行研究的人，完全是在耗费时间。

如果你知晓圆周率的后续性质，那么你的知识水平起码超越了 99.99%的人。

最近，中国科学技术大学上海研究院的墨子沙龙邀请了中国科学院数学与系统科学研究院的袁亚湘院士做了一场名为《数学漫谈》的报告（袁亚湘院士：刷题能学好数学吗？ | 墨子沙龙）。袁亚湘院士担任中国数学会的前理事长。他在这场报告的开头，讲述了许多关于π的有趣性质。

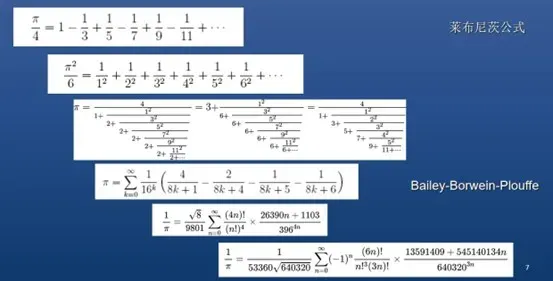
有很多意想不到的公式得到π。例如：

1 减去 1/3 ，再加上 1/5 ，接着减去 1/7 ，然后加上 1/9 ，再减去 1/11 ，以此类推……

你猜，这样无穷下去等于多少？答案是π/4。

这种方法是一种数值方法，它能够用来计算π，不过其缺点是收敛速度非常缓慢。而下面这种方法则要快得多，你可以使用它。

1 加上 1 除以 2 的平方，再加上 1 除以 3 的平方，接着加上 1 除以 4 的平方，以此类推……

你猜，这个无穷级数又等于多少？答案是π^2/6。

这两个公式相对而言较为简单，起码在我上大学的时候是学过的。倘若你能够证明它们，那么你的数学至少达到了大学的水平。然而，下面这个公式，却有着一种别样的神奇之感：

π等于从 k 等于 0 到无穷大的求和。这个求和为(1/16^k)乘以[4/(8k+1) - 2/(8k + 4) - 1/(8k +5) - 1/(8k +6)]。

我不知道这个公式的由来，但它的形式较为简单。若我努力钻研，或许能够搞明白。并且很容易能看出，这个公式收敛速度很快，因为每一项前面都有除以 16 的 k 次方，随着 k 的增大它会快速减小。

令人震惊的是，还有下面这种完全神来之笔的公式：

π 的倒数等于 8 的平方根除以 9801 乘以从 n 等于 0 到无穷大的求和，求和式为[(4n)!/(n!)^4]乘以[(26390n + 1103) / 396^(4n)]

印度传奇数学家斯里尼瓦瑟·拉马努金（Srinivasa Ramanujan，1887 — 1920）提出了这个公式。他常常能提出令人惊叹的恒等式，而这就是他的代表作之一。对于计算圆周率时会出现 26390 这么大的数，我完全无法理解其原因。希望有专家能够为我和公众进行指点。

这个公式的收敛速度更快，每进行一项计算就能得到 8 位十进制数字。1985 年，有人借助它将π计算到了 1750 万位。

可是这还没完。袁亚湘举的最后一个公式是：

1 除以π等于 1 除以[53360 乘以根号下 640320]，对 n 从 0 到无穷进行求和，即(-1)的 n 次方乘以{(6n)!除以[(n!)的 3 次方乘以(3n)!]}乘以[(545140134n + 13591409)除以 640320 的 3n 次方]

前面有了铺垫，我会对这公式的复杂程度感到震惊，不过很快就能明白，它与拉马努金公式基于相同原理，因为它们的结构相似。只要能理解拉马努金公式，就肯定能理解这个更复杂的公式，只是需要下功夫的多少不同而已。仔细看，这里最大的数是 545140134 这个九位数。然而，最特别的是 640320，它出现了两次，一次在连加前面的根号下，另一次在连加中的 3n 次方那一项。由此可以看出，这里必定有某种诀窍。

事实上，搜索后可知，这是大卫·丘德诺夫斯基和格雷高里·丘德诺夫斯基兄弟于 1989 年提出的。它是对拉马努金公式的改进。用此公式，计算一项就能得到 15 位十进制数字。1994 年，丘德诺夫斯基兄弟用该公式把π计算到了 40 亿 4400 万位。袁亚湘告知大家，最近π已算到了 105 万亿位。

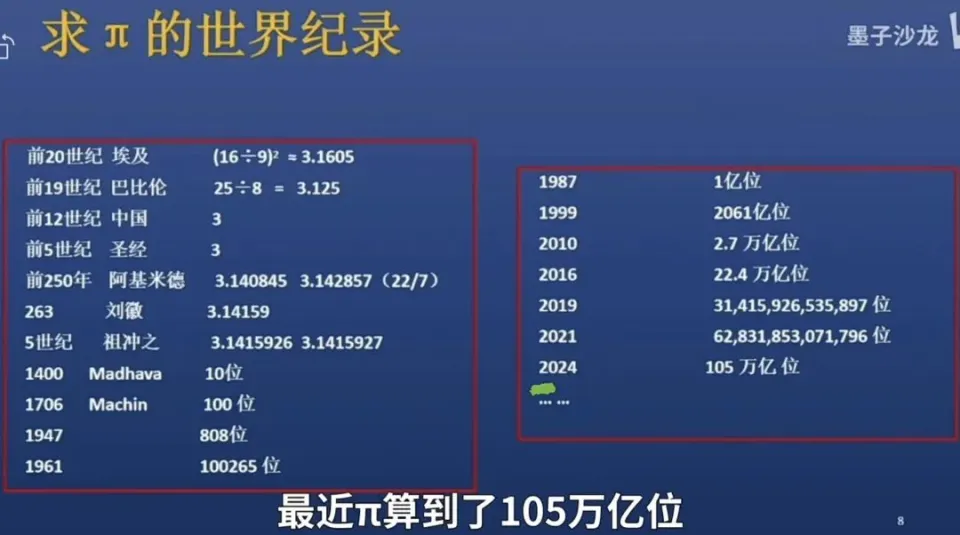
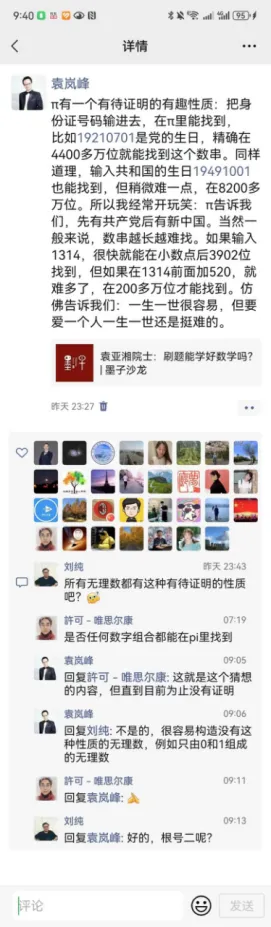
紧接着，袁亚湘提及了圆周率的一个特性。倘若你能理解他所讲的内容，那么你的知识水平便超越了 99.999%的人。

π具有一个有待证明的有趣特性：将身份证号码输入进去，在π中能够找到。例如，19210701 是党的生日，在π中精确到 4400 多万位就能找到这个数串。同理，输入共和国的生日 19491001 也能找到，不过稍微困难一些，在 8200 多万位。所以我时常开玩笑说：π告诉我们，先有共产党而后才有新中国。通常来讲，数串越长，就越难以找到。如果输入 1314，那么很快就能在小数点后 3902 位找到它。然而，如果在 1314 前面加上 520，情况就变得困难多了，需要在 200 多万位才能找到。这仿佛在告诉我们：一生一世相对而言比较容易，但要爱一个人一生一世却还是挺难的。

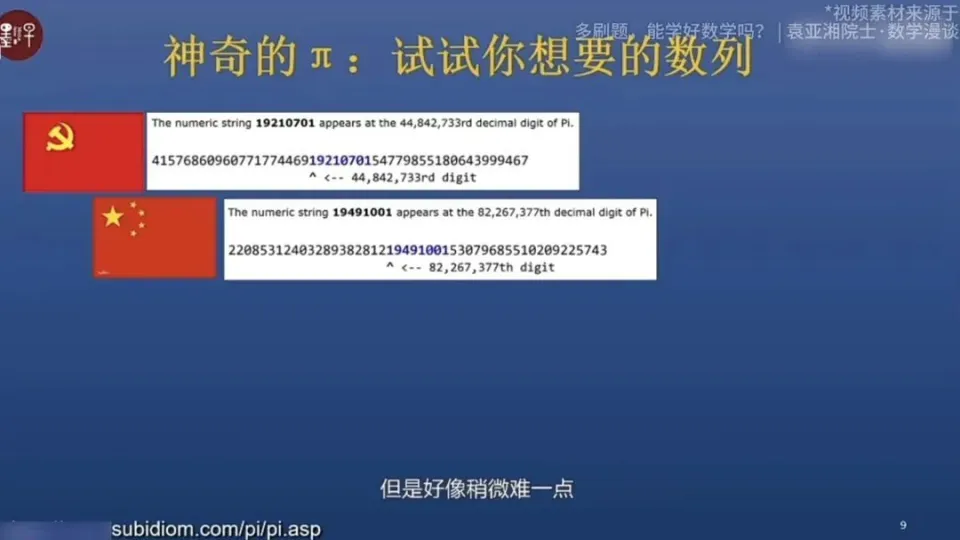
你是否明白了？袁亚湘所说的是这样一个性质：在圆周率的小数表示里，包含着所有有可能出现的自然数序列。需要注意的是，这个性质尚未得到证明，即我们不知道π是否真的包含所有的自然数序列。目前能够说的只是，我们对很多序列进行了尝试并且都找到了，并且到现在为止还没有找到反例。

再进行一次搜索，能够发现具有这样性质的数字被称作正规数。实际上，正规数的定义要比刚才所说的更严格一些，它还要求所有等长的序列出现的概率是相等的，并且都等于它们在完全随机序列中出现的概率。不过对于我们这些对数学不太了解的人来说，暂时可以不用去关注这些细节。

正规数的意义可这样理解：若将自然数序列当作一种编码，那么在正规数里能够找到各种信息。能找到你的生日，能找到你的电话号码，能找到你的所有信息。还能找到古往今来的所有书籍，所有图片，所有影视。也能找到外星人的所有信息，以及以后可能产生的任何信息。这着实令人神往，而唯一的问题就是我们没有足够的时间去浏览那么多信息。

有朋友询问，是否所有的无理数都具备这样的性质呢？答案是，显然并非如此。因为我们能够构造出一个仅仅由 0 和 1 构成的无理数：

0.101001000100001...

这个数有这样的特点：两个 1 之间的间隔在逐渐变长，依次是一个 0、两个 0、三个 0、四个 0 等等。很明显，它不是循环小数，所以它是无理数。然而，有很多序列在它当中是找不到的，比如包含 0 和 1 之外数字的序列，以及包含相连的两个 1 的序列。因此，它不是一个正规数。

朋友又问了：那根号2呢？它是不是正规数？

答案再次令人震惊。人类当下对正规数的认知处于一种很奇特的状态：一方面我们知晓其数量极为庞大，仿佛随处可见；但另一方面我们却很难举出一个确切的事例。

来看前一面。正规数特别多，这意味着我们能够证明几乎所有的实数都为正规数。“几乎所有”的含义是，非正规数的测度为 0，即非正规数在实数中所占的比例是 0。

当然，测度为 0 并不能表明不存在。很明显，非正规数大量存在。所有的有理数都是非正规数，因为它们的小数表示会循环。然而，如果你学过实数的性质，你就会知晓有理数在实数中所占的比例是 0。当然，如果能够了解这些，那么你的知识水平原本就超过了 99.99%的人。现在我们知道的是，所有的有理数在实数中所占的比例是 0。并且所有的非正规的无理数在实数中所占的比例也是 0。所以所有的有理数加上所有的非正规的无理数，在实数中所占的比例还是 0。

再来看后面这一面。随便拎出一个实数的话，它有极大的概率是正规数，实际上这个概率是 100%，因为它不是正规数的概率是 0%。然而，100%的概率并不等同于必然会发生。最神奇的是，对于像π、根号 2、ln2、e 等你容易想到的无理数，我们目前都不知道它们是不是正规数。

事实上，法国数学家埃米尔·博雷尔（Félix-Édouard-Justin-Émile Borel，1871 — 1956）在 1909 年提出了正规数这个概念。他马上证明了几乎所有的实数都属于正规数这一情况。然而，首个被知晓的正规数，得等到 1917 年才由波兰数学家瓦茨瓦夫·谢尔宾斯基（Wacław Franciszek Sierpiński，1882 — 1969）构造出来。对于那些并非专门构造出来的数，像常见的π或者根号 2 等这类数，要去判断它们是否为正规数是极为困难的。

数学里经常出现类似的窘境。比如我们知晓π和 e 都是无理数，然而对于它们俩相加是否为无理数，至今无人知晓。尽管从直觉上判断，π + e 几乎不可能是有理数，但目前却无法予以证明。

现在，你对数学的博大精深，是不是有了更多的感悟呢？