陶哲轩的最新力作在“自然数的倒数之和是否是有理数”问题上取得了一系列进展。

最引人注目的结果之一是，它证明了一个非常反直觉的猜想，它确实是正确的：

存在递增的自然数列 ak ，使得对于任何有理数 t， 都是有理数。 ( )

Topos研究所的数学物理学家约翰·卡洛斯·贝兹（John Carlos Baez）在评论区毫不掩饰自己的惊讶：

哇，这个结论太违反直觉了！但这也意味着这项研究非常有趣。

为什么这个结论如此违反直觉？

可以理解，让级数之和成为有理数是很困难的。添加任意有理数t的偏移并保持级数有理数，难度会增加几个数量级。

它需要对所有有理数 t 成立，并且有无限多个有理数。

每增加一个t就相当于增加一个约束

改变序列中的任意数字 ak 都会同时影响所有 t 对应的级数和

数学家肯尼斯·斯托拉斯基可能也有同样的想法，因此他提出了相反的斯托拉斯基猜想。

现在，陶哲轩的结论就相当于证明了斯托拉斯基猜想并不成立。

果然，数学的神奇之处在于，有时看似不可能的事情实际上是可能的，但解决方案可能超出了我们的直觉知识。

那么，陶哲轩的方法是如何颠覆直觉的呢？

迭代逼近法解决无限维问题‍‍‍‍‍‍‍‍‍‍

从论文提交历史可以看出，这项研究最初只有一位作者，Vjekoslav Kovač，研究了两个特定系列的理性问题。

陶哲轩加入后，帮助科瓦奇拓展了对整个艾哈迈斯系列的研究。

原本只有6页的短文，被扩展成了长达28页的长篇论证……

除了论文之外，陶哲轩还在个人博客上阐述了他们的想法。

我们不是直接尝试构造这个级数，而是将问题转化为研究一个集合，然后使用“迭代逼近”的方法逐步求解。

首先，我们来解释一下什么是Ahmes系列。

Ahmes级数是满足以下形式的无限级数，其中ak是自然数的严格递增序列。

由于大多数实数都是无理数，人们也会期望这样的级数“通常”也是无理数，但很难确定特定级数的无理性。

首先，数学界此前已经知道，如果aₖ的增长速度快于C(2k)（对于任何常数C），那么对应的Ahmes级数一定是无理数。

也就是说，有一条明确的“增长速度分割线”。超过这个速度，级数一定是不合理的。但接近这个速度，仍然有可能找到合理的例子。

接下来，论文表明，如果满足aₖ₊₁=O(aₖ²)，则意味着aₖ₊₁的增长速度比aₖ²慢得多。 ‍

那么就可以找到一个可比较的级数bₖ，它与aₖ渐近相关，并且Σ(1/bₖ)是一个有理数。

这部分解决了Erdős的问题#263：序列aₖ=22k是否符合这个性质，以及是否所有增长率不超过指数水平的序列都具有这个性质。

由于条件 aₖ₊₁=O(aₖ²) 不足以涵盖 aₖ =22k 的情况，因此该条件不适用于所有指数或较慢增长的序列。

即以aₖ₊₁=O(aₖ²)作为问题的分界线，“差不多”就可以彻底解决了。

此后，陶哲轩又给出了一个新的变体结论：

如果级数aₖ满足：aₖ₊₁=O(aₖ)（即下一项不会比当前项增长太快）且Σ(1/aₖ)收敛。

则可求出bₖ：bₖ=aₖ+O(1)（即bₖ与aₖ之差仅为有界常数）且Σ(1/bₖ)为有理数。

这又与 Erdő 的问题 #264 有关：

aₖ=2k时的情况就完全解决了，因为2k是指数增长。

问题的第二部分，关于 aₖ=k! 的情况，超出了当前方法的能力。

新的分界线定位于指数增长。

就像这样......一步一步迭代逼近，我们得到了 Erdős 问题 #266，这也是一个更高维度的变体。

陶哲轩避免了任何数论困难，主要依靠有理数集合的可数密度。 （具体演示过程略）

最终，斯托拉斯基猜想转化为无限维问题。

陶哲轩让维数d随k增长，但增长速度必须保持足够慢，以保证收敛性和密度。

这并不是陶解决的第一个埃尔德什问题

如前所述，陶哲轩给出结论的问题是Erdő的问题#266。

它是由沃尔夫数学奖获得者、匈牙利数学家保罗·埃尔多斯（Paul Erdős，1913年3月26日—1996年9月20日）提出的。

不过，这个问题的根源可以追溯到古埃及——

古埃及人进行分数运算时，只使用分子为1的分数。因此，这种分数也称为埃及分数，或单分子分数。

它们将所有复杂分数表示为单分子分数的总和。例如，3/4必须表示为3/4=1/2+1/4。

因此，很长一段时间（可能是几千年），数学史学家坚持认为古埃及人不使用分数；而是使用分数。现代数学家曾认为，埃及人之所以未能将算术和代数发展到更高的水平，是因为分数运算的复杂性（即必须将真分数分解为单分子分数）也是原因之一。 。

当数学家们发现其中的内容有多么丰富时，已经是两千多年之后了。

好吧，让我们回到埃尔多斯的问题和埃尔多斯本人。

埃尔多什被誉为20世纪最具创造力的数学家和数学猜想的提出者之一。 21岁时获得数学博士学位。他的论文导师也是冯·诺依曼的导师利奥波德。费耶尔）。

埃尔多什一生与 500 多名数学家合作，一生发表了约 1,525 篇数学论文，数量之大无人能及。

他一生致力于离散数学、图论、数论、数学分析、逼近论、集合论和概率论等领域的研究和提出问题。他的大部分工作集中在离散数学领域，并解决了该领域许多以前未解决的问题。解决了难题。

83 岁的埃尔多斯在华沙的一次数学会议上因心脏病去世。

正如他所希望的，他的墓志铭上写着：我终于不再愚蠢了（Végre nem butulok tovább）。

值得一提的是，Erdős 问题 #266 并不是 Terence Tao 解决的第一个与 Erdős 相关的问题。

2015年9月，陶哲轩在arXiv上发表论文《The Erdős差异问题》，宣布他证明了Paul Erdős在1930年代提出的数论猜想“Erdős差异问题”的存在。

埃尔多斯差分问题由埃尔多斯于1932年提出，困扰学术界80多年。

与数论中的许多难题一样，Erdös 差分问题描述起来很简单，但证明起来却很困难。

用简单的话解释一下：

假设您有一个由 1 和 -1（例如，通过抛硬币随机生成）和常数 C 组成的序列。您想要找到一个足够长的有限序列，以便该序列的总和大于常数 C 。

有趣的是，为了证实之前的这个猜想，陶哲轩经历了多年的手工计算和计算机尝试，甚至加入了专门研究它的团队（虽然当时失败了）。

最终，解决该问题的灵感来自于德国数学家Jwei Strosky在Tao博客上的评论，这表明Tao研究的另一个问题可能与鄂尔多斯差分问题有关。

“起初，我认为这种联系只是表面的。”但陶哲轩很快意识到，将新想法与现有结果相结合可能会证明问题。

这一事件当月发表在《自然》杂志上，标题为“数学天才解决了大师级难题”。

更有趣的是，埃尔多斯和陶哲轩的命运可以追溯到更早的时候。

1985年，72岁的埃尔多斯赴澳大利亚讲学。

在阿德莱德大学（其中中学生陶哲轩从8岁起就有1/3的时间在大学学习数学和物理课程）的安排下，当时10岁的陶哲轩结识了Erdős。

埃尔多斯仔细阅读了陶哲轩写的论文并鼓励他：“你是个好孩子，继续努力吧！”

随后，埃尔多斯还写了一封推荐信，推荐陶哲轩去普林斯顿大学攻读博士学位。

2010年，英国《卫报》评选出两千多年来“世界十大数学天才”，认为他们的革命性发现正在改变我们的世界——埃尔多斯和陶哲轩都榜上有名。

这两位数学家还有一张非常经典的照片：

2013年，在埃尔多斯诞辰100周年之际，陶哲轩在博客上分享了与埃尔多斯的珍贵合影，以表达对他的怀念和感激之情。

还有一件事

但！

尽管#266 是由Tao 得出的结论，但Paul Erdős 留下了许多未解决的问题。这些问题通常是他与其他数学家合作提出的，有些是他自己思考后形成的。

这些问题涵盖了数论、组合数学、图论、概率论等许多数学领域。

目前，860 个问题中，仍有 580 个问题等待探索（除去#266，仍有 579 个问题）。这些问题的奖金从 0 美元到 10,000 美元不等。

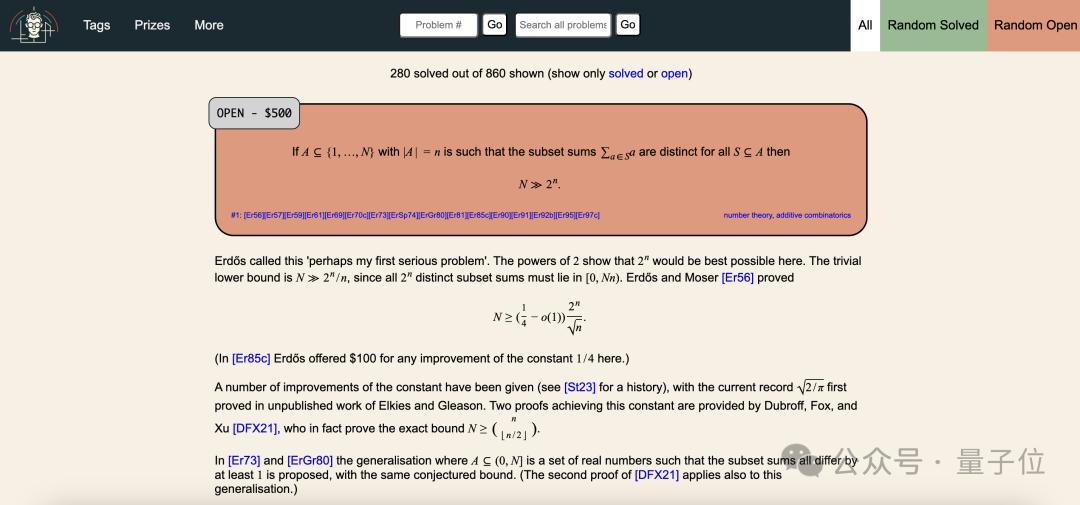
这些灿烂而迷人的遗产至今仍然激励着每一位数学家，推动着数学的进步，让后人获得新的视角和启发。

论文地址：

参考链接：

[1]@tao/113559149269764165

[2]

[3]

[4]

本文来自微信公众号“量子比特”，作者：梦辰恒宇，36氪经授权发布。